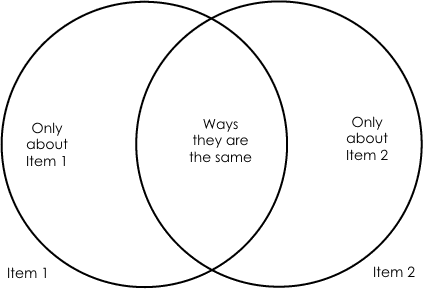
Carl sent me a link to a Venn diagrams post, so that got me thinking. A Venn Diagram with $n$ atoms has to represent $2^n$ regions. For example if $n$ is $2$, then you have the standard Venn diagram below.
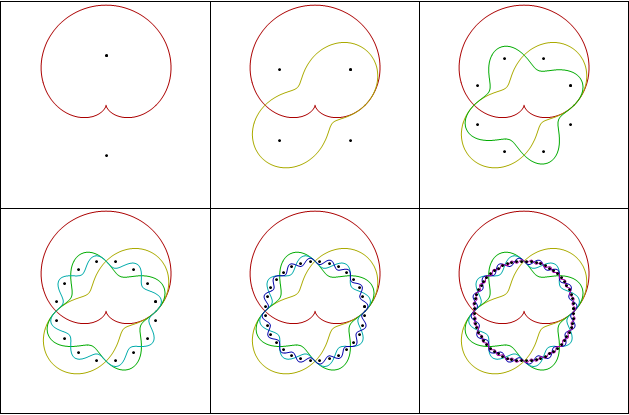
Each time you increase $n$ by one, you double the number of regions. This makes me think of binary codes and orthogonal functions. Everybody’s favorite orthogonal functions are the trig functions, so you should be able to draw Venn diagrams with wavy trig functions. Here was my first try.
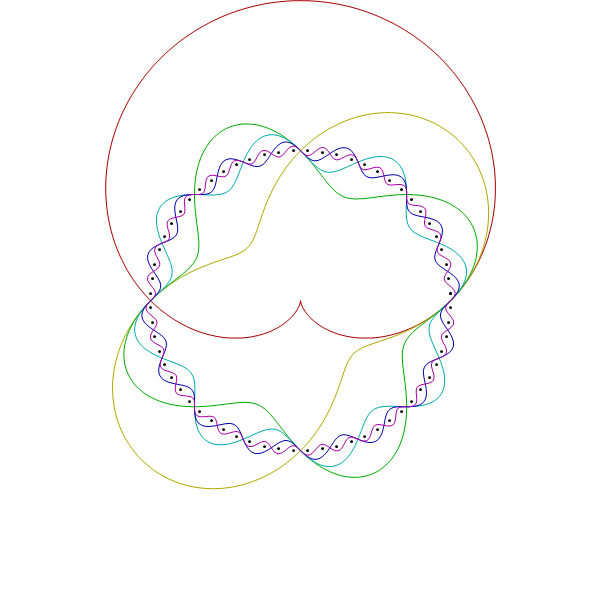
Those seemed kind of busy, so I dampened the amplitude on the high frequencies (making the slopes that same and possibly increasing artistic appeal.)
I really like the last one.