December 2020

You are currently browsing the monthly archive for December 2020.

Maximizing a function over integers (Part 3)

December 31, 2020 in Math by hundalhh | Permalink

In part 1, we defined the term strictly concave and introduced the theorem that if $f$ is strictly concave and $f(x)=f(x+1)$, then the integer(s) that maximize $f$ are exactly the set $\{\mathrm{floor}(x+1), \mathrm{ceil}(x)\}$ which is usually a set containing only one number $\mathrm{round}(x+1/2)$. In part 2, we showed how the theorem in part 1 can be used to prove that the maximum value that can be obtained when putting an integer into $f(x)=a x^2 + b x + c$ is $f(i)$ where $i=\mathrm{round}(-b/(2a))$ (assuming $a<0$).

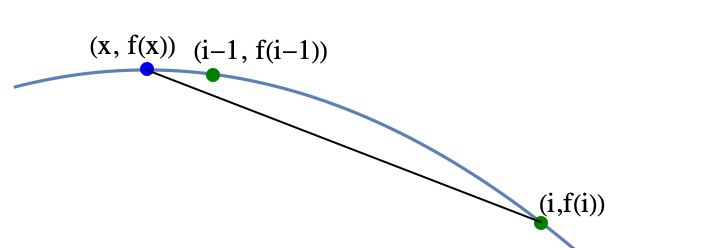
The next theorem says that the real number $x$ that maximizes $f$ is always near the integer $i$ that maximizes $f$.

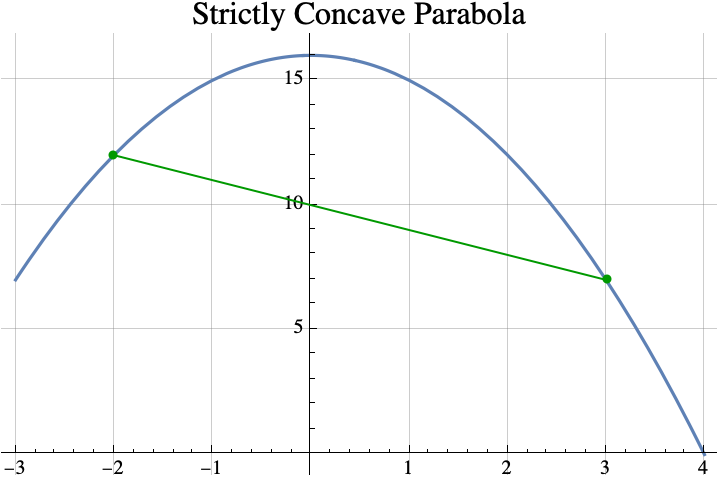
THEOREM #3

$f$ is a real valued strictly concave function,
there is a real number $x$ such that $f(x)$ is the maximum value that $f$ attains with real inputs, and
there is an integer $i$ such that $f(i)$ is the maximum value that $f$ attains with integer inputs,

then $|x-i|<1$.

The idea of the proof is fairly simple. Suppose that $i>x+1$. Then $i-1>x$. So $i-1$ is between $i$ and $x$. Concavity implies that that the point $(i-1, f(i-1))$ lies above the line connecting $(x, f(x))$ and $(i,f(i))$, but $f(x)\geq f(i)$.

The fact that the point $(i-1, f(i-1))$ is above the line implies that $f(i-1)> f(i)$, but that contradicts the definition of $i$, so using proof by contradiction, $i\leq x+1$. The other cases are either similar or easy.

EXAMPLE

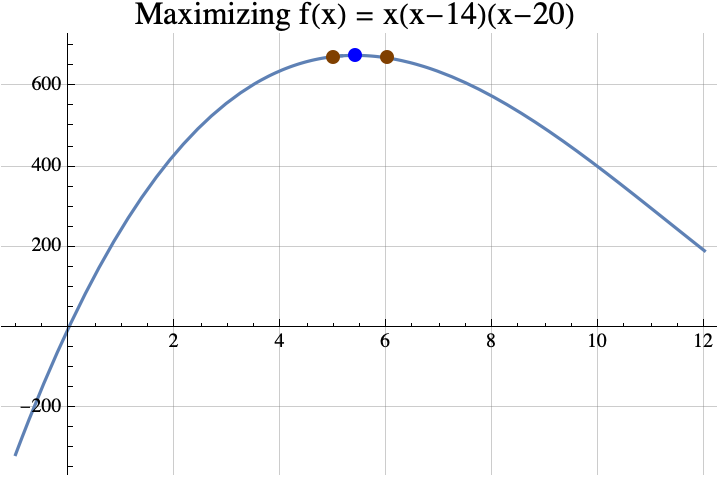
Find the maximum value of $f(x) = x (x-14) (x-20)$ among all integers between 0 and 14.

Finding the maximum among reals is easy if you know differential calculus and the quadratic formula. According to differential calculus, the maximum can only occur if the “derivative” of $f(x)$ is zero. $$f(x) = x (x-14) (x-20) =x^3-34 x^2 + 280x.$$ The derivative of a polynomial can be found by multiplying the coefficient by the exponent and decreasing the exponent by 1. The result is $$f'(x) = 3 x^2 -68 x + 280.$$ If we put that in the quadratic formula, we get $$x=\frac{68\pm\sqrt{68^2 – 4 \cdot 3 \cdot 280}}{2 \cdot 3} = \frac{68\pm\sqrt{1264}}{6}\approx 5.41\ \mathrm{or\ } 17.26.$$ It turns out that 17.26 is a local minimum, so the local maximum occurs when $x\approx 5.41$. According to the theorem, any integer $i$ that maximizes $f(i)$ must be within 1 of 5.41, so that integer can only be 5 or 6. Now $f(5)= 675$ and $f(6) = 672$, so 5 is the integer that maximizes $f$. Incidentally, $f(5.41) = 678.025021$ and the true maximum of $f(x)$ is $$f\left(\frac{68-\sqrt{1264}}{6}\right) = \frac{16}{27} \left(442+79 \sqrt{79}\right)\approx 678.025101610626.$$

We could actually use the theorem from part 1 to find the integer $i$ that maximizes $f(i)$. Solving $f(x)=f(x+1)$ using the quadratic formula gives $$x=\frac{1}{6} \left(65\pm\sqrt{1261}\right).$$ If you replace the $\pm$ with the plus sign, you get the local minimum. If you replace it with the minus sign, you get $$\frac{1}{6} \left(65-\sqrt{1261}\right)\approx 4.91.$$ According to the theorem from part 1, the integer that maximizes $f(x)$ must be round(4.91+1/2)=round(5.41)=5. Often it is easier to find the maximum of $f$ rather than trying to solve $f(x)=f(x+1)$, so that is why the theorem above is useful.

If you want to see a more formal mathematical writeup, click here. That PDF shows how you can generalize the three given theorems to a larger class of functions that are not necessarily strictly concave. Also, in the last section of the paper, we sharpen the bound on the difference between the real maximum and the integer maximum. Above, we showed that this difference was less than 1. If $f$ is continuously twice differentiable, then sharper bounds can be computed.

This concludes the three part series.

Maximizing a function over integers (Part 2)

December 26, 2020 in Math, Optimization by hundalhh | Permalink

Parabolas

The simplest concave functions are parabolas with the vertex at the top. All parabolas can be described by three real numbers $a$, $b$, and $c$, and the formula $y=a x^2 + b x + c$. For strictly concave parabolas $a<0$. For example, if $a=-2$, $b=3$, and $c=5$, then the function $y= f(x) = -2x^2 + 3 x +5$ is the parabola shown below.

If the vertex (shown above in blue) is above the x-axis, then the x-coordiante of the vertex can be computed by finding the points where the concave parabola crosses the x-axis (shown above in orange). In our case, the parabola $y=f(x)$ crosses the x-axis when $0=y=f(x)$, or when $$\begin{aligned}0&= -2x^2 + 3 x +5\\0&=-(2x^2-3×-5)\\0&=-(2×-5)(x+1).\end{aligned}.$$ If $0=\alpha\cdot \beta$, then either $\alpha=0$ or $\beta=0$. So, the parabola crosses the x-axis when either $0=2×-5$ or $0=x+1$ which means that it crosses when $x=5/2$ or $x=-1$. Parabolas are symmetric about the vertical line going through the vertex, so the x-coordinate of the vertex is half way between the x-coordinates of the crossing points (a.k.a the roots of $f(x)$). $$\begin{aligned} x_\mathrm{vertex} &= \frac{x_\mathrm{crossing1} + x_\mathrm{crossing2}}2\\&= \frac{ -1 +5/2}2\\&=\frac{3/2}2\\&=3/4.\end{aligned}$$

So the x-coordinate of the vertex is $x=3/4$. This is also the real number that maximizes $f(w)$ over all real numbers $w$.

In general, the x-coordinates of the crossing points can be found with the quadratic formula $$x=\frac{-b\pm\sqrt{b^2-4ac}}{2 a}.$$ The $\pm$ sign means that one crossing can be found by replacing $\pm$ with + and the other can be found by replacing the $\pm$ with -. But, if you have one number that is $x_1=\alpha+\beta$ and another that is $x_2=\alpha-\beta$, then the average of the two numbers is just $\alpha$. In other words if the two values of $x$ are $x=\alpha\pm\beta$, then the average value is just $\alpha$. So, to computer the average x-coordinate of the crossing points, all we have to do is remove the $\pm$ sign and whatever it is applied to from the quadratic formula. $$ x_\mathrm{vertex} = \frac{-b}{2 a}.$$

theorem #2

Informally, if $y=f(x)$ is a parabola, $f(x) = a x^2 + b x + c$, and $a<0$, then the integer(s) that maximize $f(x)$ are the set $\{\mathrm{floor}(x+1/2), \mathrm{ceil}(x-1/2)\}$ where $x=\frac{-b}{2 a}$.

If $x$ is an integer plus 1/2 (e.g. 2.5, 7.5, …), this set has two elements $x+1/2$ and $x-1/2$. If $x$ is not an integer plus 1/2, the set has only one element $\mathrm{round}(x)$ and that is the integer that produces the highest possible value of $f(z)$ among all integers $z$.

examples

Example 1: If $f(x)= -2x^2 + 3 x +5$, then $a=-2$, $b=3$, and $c=5$. The values of $x$ in the theorem is the same as the x-coordinate of the vertex $$x=\frac{-b}{2a} = \frac{-3}{2\cdot(-2)}= \frac{-3}{-4}=3/4.$$ The integer(s) that maximize $f(z)$ among all integers $z$ are the set $$\begin{aligned}\{\mathrm{floor}(x+1/2), \mathrm{ceil}(x-1/2)\}&= \{\mathrm{floor}(3/4+1/2), \mathrm{ceil}(3/4-1/2)\}\\&= \{\mathrm{floor}(5/4), \mathrm{ceil}(1/4)\}\\&=\{1\}.\end{aligned}$$

Example 2: If we lower the parabola from example 1 by a little bit setting $f(x)= -2x^2 + 3 x +\sqrt{17}$, then $a=-2$, $b=3$, and $c=\sqrt{17}$. The value of $x$ in the theorem is the same as the x-coordinate of the vertex $x=\frac{-b}{2a} =3/4.$ The result does not depend on $c$, so as in example 1, the integer that maximizes $f(z)$ among all integers $z$ is $z=\mathrm{round}(3/4)=1$.

Example 3: $f(x)= -x^2+x = (1-x)x$, then $a=-1$, $b=1$, and $c=0$. The value of $x$ in the theorem is the same as the x-coordinate of the vertex $$x=\frac{-b}{2a} =\frac{-1}{2\cdot (-1)}=1/2.$$ The integer(s) that maximize $f(z)$ among all integers $z$ are the set $$\begin{aligned}\{\mathrm{floor}(x+1/2), \mathrm{ceil}(x-1/2)\}&= \{\mathrm{floor}(1/2+1/2), \mathrm{ceil}(1/2-1/2)\}\\&= \{\mathrm{floor}(1), \mathrm{ceil}(0)\}\\&=\{1,0\}.\end{aligned}$$ The integers that maximize $f(z)$ among all integers $z$ are 0 and 1. If we look at the graph of $f(x)$ below, we can see that the graph crosses the x-axis at $x=0$ and $x=1$. So, $f(0)=f(1)=0$. All other integers inputs produce negative values.

the spirit of the proof

It turns out that Theorem 2 can be proven from theorem 1. Recall that in Theorem 1, we wanted to find the value of $x$ where $f(x)=f(x+1)$. If we found that value, then the integer(s) that maximize $f$ are exactly the set $\{\mathrm{floor}(x+1), \mathrm{ceil}(x)\}$. In Theorem 2, $f(x) = a x^2 + b x + 1$. So if $f(x)=f(x+1)$, then $$\begin{aligned}a x^2 + b x + c &= a (x+1)^2 + b (x+1) + c\\a x^2 + b x &= a (x+1)^2 + b (x+1)\\ a x^2 + b x &= a (x^2+2x+1)+ b x+b\\ a x^2 &= a x^2+2ax+a+ b \\ 0 &= 2ax+a+ b \\ -a-b &= 2ax \\ \frac{-a-b}{2a} &= x\\ \frac{-b}{2a}-\frac12 &= x\\\end{aligned}.$$

Thus the integers that maximize $f(x)$ must be $$\begin{aligned} \{\mathrm{floor}(x+1), \mathrm{ceil}(x)\ \}&= \{\mathrm{floor}(\frac{-b}{2a}-\frac12+1), \mathrm{ceil}(\frac{-b}{2a}-\frac12)\} \\ &= \{\mathrm{floor}(\frac{-b}{2a}+\frac12), \mathrm{ceil}(\frac{-b}{2a}-\frac12)\}.\end{aligned}$$

Why DId I WANTED to know this

I was looking at several games where the optimal strategy depended on finding an integer $t$ that maximized $f(t)$. In the game Slay the Spire, I wanted to maximize the amount of poison damage that I was going to do with the cards “Noxious Fumes” and “Catalyst”. If I played the “Catalyst” on turn $t$ and the combat ended on turn $T$, then the poison damage done was $$\frac{(t+1)t}{2} -1 + (T-t)t$$ where $ \frac{(t+1)t}{2}-1$ (note the triangle number) was the damage done by “Noxious Fumes” and $ (T-t)t$ was the additional damage done by playing the Catalyst. I wanted to maximize $f(t) = (T-t)t = -t^2 + T t$.

Using Theorem 2, $a=-1$, $b=T$, and $c=0$. The Theorem says that the maximum damage occurs when you play the “Catalyst” on round $t$ where $t$ is contained in the set $\{\mathrm{floor}(x+1/2), \mathrm{ceil}(x-1/2)\}$ with $x=\frac{-b}{2 a}$. So $x=\frac{-T}{2\cdot(-1)}=T/2$. The best time to play the Catalyst was around half way through the combat. The catalyst should be played on round $T/2$ if $T$ is even. If $T$ is odd, then the best round to play the “Catalyst” was for $t$ in the set $$\{\mathrm{floor}(T/2+1/2), \mathrm{ceil}(T/2-1/2)\}= \{\frac{T+1}{2}, \frac{T-1}{2} \}.$$

summary

So the first two theorems formalized two rules of thumb:

If you can find an $x$ where $f(x)=f(x+1)$, then the optimal integer(s) is $z=\mathrm{round}(x+1/2)$ with a special round that provides two answers if $x$ is an integer, and
If $f(x)=a x^2 + b x + c$ (a parabola), then the optimal integer(s) is $z=\mathrm{round}(x)$ where $x=\frac{-b}{2 a}$ which is the $x$ that maximizes $f(w)$ over all real numbers $w$ (i.e. the x-coordinate of the vertex).

If you want to see a more formal mathematical writeup, click here.

Maximizing a function over integers (Part 1)

December 25, 2020 in Math, Optimization by hundalhh | Permalink

I proved a few simple but interesting theorems about integers that maximize a function $f$ when $f$ is a strictly concave function that maps real numbers to real numbers. For example, the real number that maximizes $f(x)=x(1-x)$ is $x=1/2$, but among all the integers, the maximum possible value of the function is 0. And that maximum is achieved twice with integers 0 and 1, $f(0)=0=f(1)$.

A function is strictly concave if you can pick any two points on its graph, draw a line between them, and the curve $y=f(x)$ between the two points lies entirely above the line between the two points.

Theorem #1

Informally stated, the first theorem is that if you can find a real number $x$ such that $f(x)=f(x+1)$, then the integer(s) that maximize the concave function $f$ are the set $\{\mathrm{floor}(x+1), \mathrm{ceil}(x)\}$ where “floor” just means round down and “ceil” means round up. That set usually contains only one element which is $\mathrm{round}(x+1/2)$, but if $x$ is an integer, then it will contain two consecutive integers $x$ and $x+1$.

For example, if $f(x) = 4-4x^2$, then the value of $x$ that satisfies $f(x)=f(x+1)$ is $x=-1/2$ because $f(-1/2)=3=f(1/2)$. So the theorem says that any integer that maximizes $f$ must be in the set $$\begin{aligned}\{\mathrm{floor}(x+1), \mathrm{ceil}(x)\} &= \{\mathrm{floor}(-1/2+1), \mathrm{ceil}(-1/2)\}\\&= \{\mathrm{floor}(1/2), \mathrm{ceil}(-1/2)\} \\&= \{0\}.\end{aligned}$$ The integer that does the best is 0 which is also the real number that maximizes $f$.

Here is another example. If $f(x) = \sin(x)$, then the value of $x$ that satisfies $f(x)=f(x+1)$ is $x=1.0708$ because $f(1.0708)=0.877583=f(2.0708)$. So the theorem says that any integer that maximizes $f$ must be in the set $$\begin{aligned}\{\mathrm{floor}(x+1), \mathrm{ceil}(x)\} &= \{\mathrm{floor}(1.0708+1), \mathrm{ceil}(1.0708)\}\\&= \{\mathrm{floor}(2.0708), \mathrm{ceil}(1.0708)\} \\&= \{2\}.\end{aligned}.$$ The integer that does the best is 2.

So, that was the first theorem. In part 2, we state a second theorem about finding the integer which maximizes a quadratic with some examples and one application the game “Slay the Spire”.