So, I noticed Brian Rushton’s question on matheducators.stackexchange.com. He asked,
“What should be included in a freshman ‘Mathematics for computer programmers’ course?”
User dtldarek had a pretty cool reply broken up into three parts:
- Math that is actually useful.
- Math that you can run into, and is generally good to know.
- Math that lets you build more awesome math.
His answer got me to think about and revise my “100 Most useful Theorems and Ideas in Mathematics” post. I wondered which of the 100 I used every week. Rather than trying to think about every week, I just thought it would be interesting to identify which ideas and theorems I used this week excluding the class I am teaching.
The first several ideas on the top 100 list, you can’t seem to avoid: counting, zero, decimal notation, addition, subtraction, fractions, and negative numbers. Everyone uses these ideas when they buy anything or check their change. (I wonder how many people rarely count the change from the cashier.)
The next group was mostly about algebra: equality, substitution, variables, equations, distributive property, polynomials, and associativity. Every week I attend two math seminars (Tensor Networks and Approximation Theory), so I use these ideas every week, just to add to the discussion during the seminar.
Strangely, I can’t remember using scientific notation this week except while teaching. During class, I briefly mentioned the dinosaur killing asteroid (see the Chicxulub crater). It’s hard to calculate any quantity about the asteroid (energy = 4 ×1023 Joules, mass = 2 ×1015 kg ?, velocity $\approx$ 20000 meters/sec) without using scientific notation. But, other than during class, I don’t remember using scientific notation.
During the Approximation Theory Seminar, we discussed polynomial approximations to the absolute value function so we used polynomials, infinity, limits, irrational numbers (square roots), the idea of a function, inequalities, basic set theory, vector spaces esp. Hilbert/Banach Spaces, continuity, Karush–Kuhn–Tucker conditions, linear regression, the triangle inequality, linearity, and symmetry during our discussion. That seems like a lot, but when you have been using these ideas for decades, they are just part of your vocabulary.
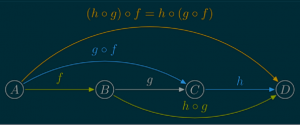
So between the approximation theory seminar and daily restaurant mathematics, I used most of the first 40 items from the top 100 list. Earlier in the week, I wrote up a simple category theory proof about isomorphisms and pull-backs. Turns out, if you pullback an isomorphism and another arrow, then you get another isomorphism. For example, in the commutative diagram below the top arrow and the bottom arrow are both isomorphisms (isometries even) and the entire diagram is a pullback. If the bottom arrow is an isomorphism and the entire diagram is a pullback, then the top arrow is an isomorphism. (The reverse is not true.)
Working on the proof got me thinking about trig functions, modular arithmetic, injective/surjective functions, Fourier transforms, duality, eigenvalues, metric spaces, projections, the Reiz Representation Theorem, Plancherel’s theorem, and numerical integration.
Probability and information theory were largely missing from my week until I stopped by Carl’s house yesterday. He and I got into a discussion about category theory, information theory, and neural networks. One thing we noticed was that 1-1 functions are the only functions that conserve the entropy of categorical variables. For example, if $X\in\{1,2,3,4,5,6\}$ is a die roll, then $Y=f(X)$ has the same entropy as $X$ only if $f$ is 1-1. Turns out you can characterize many concepts from Category theory using entropy and information theory. So we used random variables, probability distributions, histograms, the mean (entropy is the mean value of the log of the probability), standard deviations, the Pythagorean theorem, statistical independence, real numbers, correlation, the central limit theorem, Gaussian Distributions (the number e), integrals, chain rule, spheres, logarithms, matrices, conic sections (the log of the Gaussian is a paraboloid), Jacobians, Bayes Theorem, and compactness.
I almost avoided using the Pigeon Hole Principle, but then Carl argued that we could use the definition of average value to prove Pigeon Hole Principle. I still don’t feel like I used it, but it did come up in a discussion.
Notably missing from my week were (surprisingly): derivatives, volume formulas (volume of a sphere or cube), Taylor’s theorem, the fundamental theorem of calculus, and about half of the ideas between #63 Boolean algebra and #99 uncountable infinity.
So, it looks like I typically use around 70 ideas from the list each week—more than I thought.
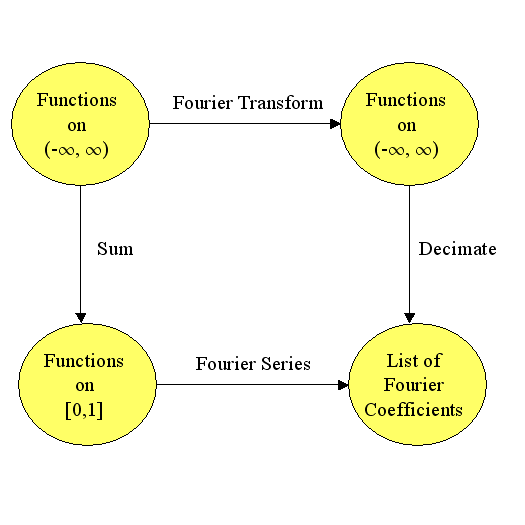
I will probably get back to 2048 stuff later this month and maybe a post on Fourier Transforms.
Have a great day! – Hein