Last month I wrote a post about the fact that you should not make an investment in a game that does not pay for itself. If an investment costs $I$ and gives you a return of $i$ per turn, then it will pay for itself in $I/i$ turns. The return on investment (ROI) is $$r= i/I.$$ In some games we have several choices about how to invest, and generally speaking it is best to choose the investments with the best ROI.
If you can invest on any turn, the ROI investment rule of thumb is,
“Don’t invest if there are less than $$I/i=1/r$$ turns in left in the game excluding the current turn.”
the tank game
The tank game is one of the simplest investment games. It illustrates a few common ideas in investment games:
- Exponential Sharpening of the Axe
- The optimal investment choice often depends only on the ROI for the turn and the number of turns left in the game.
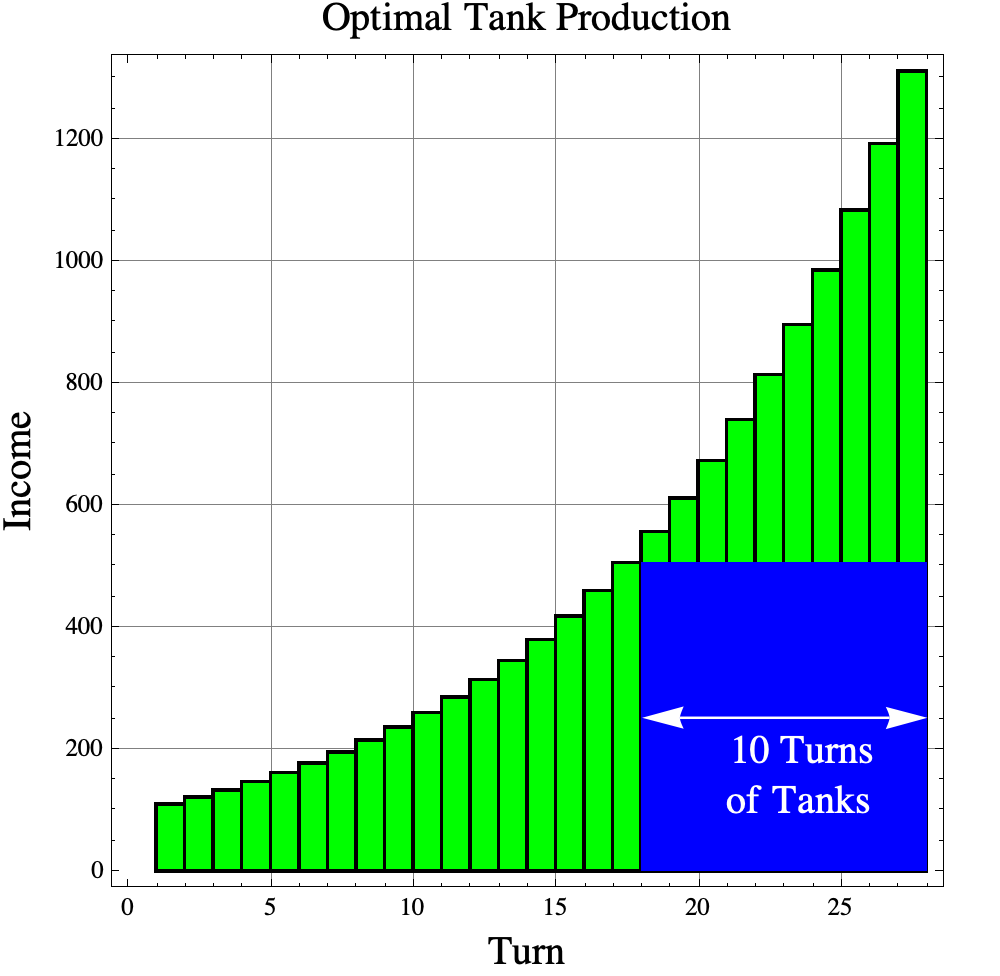
- Solving an investment game often involves finding the largest rectangle under the investment curve.
- The investment-exploitation phase transition, dominating strategies, comparing two very similar strategies, null moves, and strategy swaps
- Actually proving that a strategy is correct is a bit tricky.
- Discrete vs. Continuous.
I will address some of these ideas in this post and the rest of the ideas in a follow up post.
Suppose that you start the game with an income of \$100 million per turn. Each turn you have the two choices:
- (investment option) investing all your income into factories and increasing your income by 10%, or
- (don’t invest option) building tanks that cost one million dollars each.
Assume that it is also possible to build half a tank, or any other fraction of a tank, so if you spend \$500,000 on tanks, you get 0.5 tanks. If you spend \$2,300,000 on tanks, then you get 2.3 tanks. The game lasts for 27 turns and the object of the game is to maximize the number of tanks created.
Intuitively, you want to build up your factories in the first part of the game (Invest/Growth phase), and then transition to making tanks in the later part of the game (Exploitation phase).
Suppose that you build factory equipment for the first 5 turns, and then spend 22 turns building tanks. After the first turn, you have \$110 million income (\$100 million original income plus \$10 million income due to the investment into factory equipment). After the second turn, your income would be \$121 million (\$110 million at the start of the turn plus \$11 million additional income due to investment). After the third turn you would have \$133,100,00 income, the fourth \$146,410,000 income, and finally, at the end of the 5th turn, your income would be \$161,051,000 per turn. If you then build tanks for 22 turns, then you would have $$22\cdot161.051 = 3543.122\ \ \mathrm{tanks}$$ at the end of the game.
The optimal strategy for the tank game using the rule of thumb
The easy way to find the optimal strategy is to apply the ROI investment rule of thumb. We should invest as long as there are more than $I/i=1/r$ turns in the game after the current turn. In the tank game, you increase your income by 10% if you invest, so $r=0.10$ and $$1/r=10\ \ \mathrm{turns.}$$ On turns 1 through 16 there are more than 10 turns left in the game, so you must invest on those turns. On turn 17, there are exactly 17 turns left in the game, so it does not matter whether or not you invest on that turn. On turns 18, 19, … 27, there are less than 10 turns left in the game, so on those turns, you need to build tanks.
If you do invest for 17 turns, then your income would be $$\mathrm{income} = (1.1)^{17}\cdot \ \$100,000,000= \$ 505,447,028.50$$ per turn. Then you could buy tanks for 10 turns giving you about 5054.47 tanks.
Notice that the amount of money spent on tanks is the same as the area of a rectangle with height equal to the income at the end of the investment phase (turn 17) times the number of turns used to buy tanks. Many investment problems are equivalent to finding the largest rectangle that “fits” under the income curve.
The investment-exploitation phase transition and dominating strategy swaps
If you actually want to prove that this is the optimal strategy, you should probably first prove that there is and investment phase followed by a building/exploitation phase.
We will prove that investment phase must come first by comparing two very similar strategies where we swap a Building action and an Investing action. Comparing two similar strategies and showing the one “dominates” the other is a common tactic for finding optimal strategies. In game theory, we say that one strategy dominates another if it is always better no matter what the opponent does. For the single player tank game, we will say that one strategy dominates another if it produces more tanks over the course of the game.
Option 1: Build-then-Invest. Suppose that on turn $i$ that you build tanks and on turn $i+1$ you invest in factories. Suppose that on turn $i$ that your income was $I$. Then you would build $$\mathrm{tanks} = \frac{I}{\$1,000,000}$$ tanks on turn $i$ and your income would increase to on turn $i+1$ to $$I_{\mathrm{new}}=1.1\ I.$$
Option 2: Invest-then-Build. On the other hand, if you swap the two strategies on turns $i$ and $i+1$, then on turn $i$ your income would again increase to $$I_{\mathrm{new}}=1.1\ I,$$ but when you build the tanks on turn $i+1$ you end up with $$\mathrm{tanks} = \frac{I_{\mathrm{new}}}{\$1,000,000}= \frac{1.1\ I}{\$1,000,000}.$$
For either option, you have the same income on turns $i+2, i+3, \ldots, 27$, but for Option 2 (Invest-then-build) you have 10% more tanks than option 1. We conclude that Option 2 “dominates” option 1, so for the optimal strategy, a tank building turn can never precede an investment turn. That fact implies that there is an investment phase lasting a few turns followed by an building phase where all you do is build tanks.
If we carefully apply the ideas in the ROI part 1 post, we can determine where the phase transition begins. Suppose that on turn $i$ we have income $I$ and we make our last investment to bring our income up to $1.1\ I$. The increase in income is $0.1\ I$ and that new income will buy $$\mathrm{tanks\ from\ new\ income} = \frac{0.1\ I (T-i)}{\$1,000,000}$$ new tanks where $T=27$ is the total number of turns in the game. If we build tanks instead of investing on turn $i$ then we would make $$\mathrm{potential\ tanks\ on\ turn\ }i = \frac{I}{\$1,000,000}$$ tanks. The difference is
$$\begin{aligned} \mathrm{gain\ by\ investing} &= \frac{0.1\ I (T-i)}{\$1,000,000}\; – \frac{I}{\$1,000,000}\\ &= \frac{0.1\ (T – i) \;- I}{\$1,000,000}.\end{aligned}$$
The gain is positive if and only if $$\begin{aligned} 0.1\ I (T-i) – I &> 0\\ 0.1\ I (T-i) &> I\\ 0.1\ (T-i) &> 1\\T-i &> 10\\T-10&> i.\end{aligned}$$
Remark: Reversing the inequalities proves that the gain is negative ( a loss) if and only if $T-10 < i$.
We conclude that no tanks can be built before turn $T-10=17$. On turn $i=17$, $$0.1\ I (T-i) -I = 0.1\ I (27-17) -I = 0,$$ so the gain by investing is zero. It does not matter whether the player builds tanks or invests on turn 17. After turn 17, the gain is negative by the Remark above, so you must build tanks after turn 17.
We have proven that the ROI investment rule of thumb works perfectly for the tank game.