October 2012

You are currently browsing the monthly archive for October 2012.

K medians & K-medoids

October 30, 2012 in Clustering by hundalhh | Permalink

K-medians and K-medoids are a variants of K-means clustering algorithm. The both minimize the sum of the distances from the centroids to the points, but the K-modoids algorithm requires that the center of each cluster be a sample point. Both problems can be solved using EM type methods.

“Active Learning Literature Survey”

October 28, 2012 in Reinforcement Learning by hundalhh | Permalink

In “Active Learning Literature Survey“, Burr Settles (2010) reviews uncertainty sampling (Lewis and Gale, 1994), margin sampling (Scheffer et al., 2001), entropy sampling, optimal experimental design, query-by-committee (Seung et al., 1992), query-by-boosting, query-by-bagging, expected model change, expected error reduction, expected information gain, variance reduction, and density weighted methods. He then comments on theoretical and empirical performance of these methods, practical considerations, and related areas of machine learning including: semi-supervised learning, reinforcement learning, and compression.

Jensen-Shannon divergence

October 26, 2012 in Information Theory by hundalhh | 2 comments

The Jensen-Shannon divergence is a symmetric version of the Kullback-Leibler divergence. Unlike the KL-divergence, the square root of the JS-divergence is a true metric obeying the triangle inequality. Interestingly, if $X$ is a random variable chosen from the average of two distributions $Q$ and $R$, then the J-S divergence between $Q$ and $R$ is equal to the mutual information between $X$ and the indicator function $I$, where $P(I=1) = q(X)/( q(X) + r(X) )$, $q(x)$ is the density of $Q$, and $r(x)$ is the density of $R$. (One immediate consequence is the JS divergence is always less than 1.)

“Hashing Algorithms for Large-Scale Learning”

October 24, 2012 in Uncategorized by hundalhh | Permalink

In “Hashing Algorithms for Large-Scale Learning” Li, Shrivastava, Moore, and Konig (2011) modify Minwise hashing by storing only the $b$ least significant bits. They use the $b$ bits from $k$ hashing functions as features for training a support vector machine and logistic regression classifiers. They compare their results against Count-Min, Vowpal Wabbit, and Random hashes on a large spam database. Their algorithm compares favorably against the others.

“Variance Reduction in Monte-Carlo Tree Search”

October 22, 2012 in Games, Reinforcement Learning by hundalhh | Permalink

In “Variance Reduction in Monte-Carlo Tree Search” Veness, Lanctot, and Bowling (2011) “examine the application of some standard techniques for variance reduction in” MonteCarlo Tree Search. The variance reduction techniques included control variates, common random numbers, and antithetic variates. These techniques were applied to three games: Pig, Can’t Stop, and Dominion. After reviewing Markov Decision Process and Upper Confidence Trees (UCT), they describe the variance reduction techniques and display charts showing the improvement of UCT for each technique and each game. The simplest game, Pig, gained the most from the variance reduction techniques, but all of the games gained from all of the techniques except no effective antithetic variate was found for Dominion.

Matlab code and a Tutorial on DIRECT Optimization

October 20, 2012 in Optimization by hundalhh | 3 comments

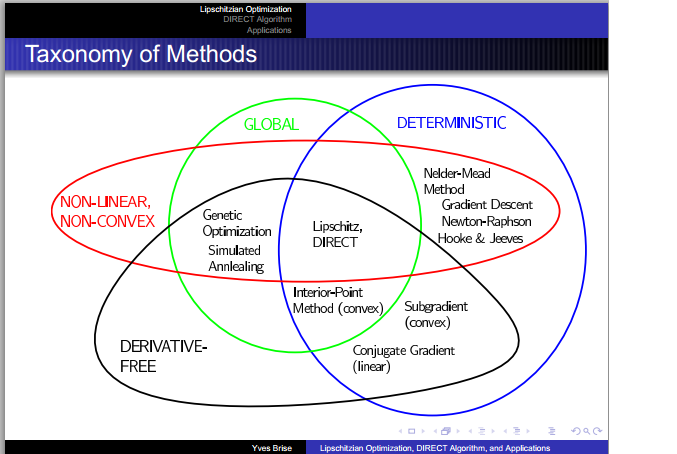
Yves Brise created this nice set of slides describing the DIRECT algorithm for Lipschitz functions. Tim Kelly of Drexel university provides Matlab code here.

“Optimistic Optimization of a Deterministic Function without the Knowledge of its Smoothness”

October 18, 2012 in Multi-Armed Bandit Problem, Optimization by hundalhh | Permalink

In “Optimistic Optimization of a Deterministic Function without the Knowledge of its Smoothness“, Remi Munos (2011) develops an optimization algorithm similar to hierarchical optimistic optimization, Lipschitz optimization, the Zooming algorithm (Klienberg, Slivkins, & Upfal 2008), branch and bound, and the upper confidence bound algorithm. The algorithm does not minimize regret, rather it attempts to maximize $\max_n f(x_n)$ over all the samples $x_n$. Munos’s first algorithm, Deterministic Optimistic Optimization, requires that the function be smooth with respect to a known semi-metric. His second algorithm, Simultaneous Optimistic Optimization, does not require knowledge of the smoothness semi-metric. He proves performance bounds, gives examples for both algorithms, and finishes the paper by comparing the algorithm to the well known DIRECT (DIviding RECTangles) algorithm (Jones, Perttunen, Stuckman 1993).

“A Tutorial on the Cross-Entropy Method”

October 16, 2012 in Optimization, Reinforcement Learning by hundalhh | Permalink

In “A Tutorial on the Cross-Entropy Method” De Boer, Kroese, Mannor, and Rubinstein (2005) write

“The CE method was motivated by an adaptive algorithm for estimating probabilities of rare events in complex stochastic networks (Rubinstein, 1997), which involves variance minimization. It was soon realized (Rubinstein, 1999, 2001) that a simple cross-entropy modiﬁcation of Rubinstein (1997) could be used not only for estimating probabilities of rare events but for solving difﬁcult COPs as well. This is done by translating the “deterministic” optimization problem into a related “stochastic” optimization problem and then using rare event simulation techniques similar to Rubinstein (1997). Several recent applications demonstrate the power of the CE method (Rubinstein, 1999) as a generic and practical tool for solving NP-hard problems.”

and then go on to compare cross-entropy with simulated annealing, tabu search , genetic algorithms, the nested partitioning method, ant colony optimization, rare event estimation algorithms, importance sampling, and algorithms for continuous multi-extremal optimization.

Several applications are listed in the introduction.

“An increasing number of applications is being found for the CE method. Recent publications on applications of the CE method include: buffer allocation (Alon et al., 2005); static simulation models (Homem-de-Mello and Rubinstein, 2002); queueing models of telecommunication systems (de Boer, 2000; de Boer, Kroese, and Rubinstein, 2004); neural computation (Dubin, 2002, 2004); control and navigation (Helvik and Wittner, 2001); DNA sequence alignment (Keith and Kroese, 2002); scheduling (Margolin, 2002, 2004); vehicle routing (Chepuri and Homem-de-Mello, 2005); reinforcement learning (Mannor, Rubinstein, and Gat, 2003; Menache, Mannor, and Shimkin, 2005); project management (Cohen, Golany, and Shtub, 2005); heavy-tail distributions (Asmussen, Kroese, and Rubinstein, 2005); (Kroese and Rubinstein, 2004); CE convergence (Margolin, 2005); network reliability (Hui et al., 2005); repairable systems (Ridder, 2005); and maxcut and bipartition problems (Rubinstein, 2002).”

The rest of the paper describes the basic CE algorithm, its convergence properties, specific applications, and variations.

Tetris, Reinforcement Learning, The Cross-Entropy method

October 14, 2012 in Games, Optimization, Reinforcement Learning by hundalhh | Permalink

Tetris is hard, but it is good for your brain. So machine learners have written a number of papers about the application of reinforcement learning to Tetris. Donald Carr (2005) reviews a number of algorithms for Tetris including temporal difference learning, genetic algorithms (Llima, 2005), hand-tuned algorithms specific to Tetris (Dellacherie, Fahey). Szita and Lörincz (2006) in “Learning Tetris Using the Noisy Cross-Entropy Method” use noise to prevent early suboptimal convergence of the fascinating cross entropy method (similar to particle swarm optimization). Much like chess, the value of the current state of a Tetris game is estimated with a linear combination of 22 features (for more details, check out the seminal Tetris paper “Feature-Based Methods for Large Scale Dynamic Programming” by Bertsekas and Tsitsiklis 1996.) Their noisy CE method produced solutions almost as good at the best contemporaneous hand-tuned Tetris algorithms.