So I have been reading a number of texts in my quest to learn category theory and apply it to AI. Two of the most interesting introductions to category theory are “Category Theory for Scientists” by Spivak (2013) and “Ologs: A Categorical Framework for Knowledge Representation” by Spivak and Kent (2012).
Ologs are a slightly more sophisticated, mathematical form of semantic networks.
Semantic networks are a graphical method for representing knowledge. Concepts are drawn as words (usually nouns) in boxes or ovals. Relationships between concepts are depicted as lines or arrows between concepts. (In graph theory, theses would be called edges.) Usually, the lines connecting concepts are labeled with words to describe the relationship. My favorite semantic network is the semantic network describing the book “Gödel Escher Bach“, but here is a simpler example.
A Semantic Network
Mathematically, semantic networks are a graph where the nodes are concepts and the edges are relationships. There are some cool algorithms for constructing semantic networks from text (see e.g. “Extracting Semantic Networks from Text via Relational Clustering” by Kok and Domingos (2008)).
Though semantic networks look like probabilistic graphical models (PGMs, a.k.a. Bayesian networks), they are different. In PGMs, the nodes are random variables not general classes and if five edges point to a node, then there is an associated five parameter, real-valued function associated with those five edges indicating the likelihood that the target variable has a particular value.
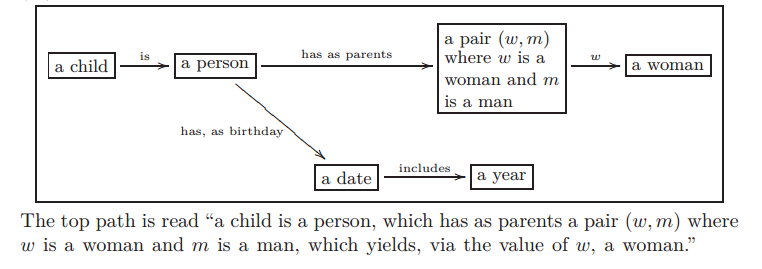
As I said before, Ologs are a more sophisticated directed graph. In Ologs, the nodes are typically nouns that can be assigned to one of many values. In directed graphs the edge starts at one node called the tail and ends at another node called the head. The edges in Ologs represent functions that given a value with the type of the tail node give you one value with the type of the head node. In the example shown below, the box “a date” could be assigned the values “Oct 12, 2010″ or “January 5, 2011″. The corresponding values of the “a year” would be 2010 and 2011.
Example Olog from “Ologs: A categorical framework for knowledge representation”
In category theory, categories are directed graphs where the edges are called arrows and they have some specific properties. Ologs are part of the category Set. One of the important properties of arrows is that if the head of one arrow is the tail of another arrow, then a third arrow is implied which is called the composition of the original two arrows. In the diagram above the arrows “has, as birthday” and “includes” can be combined to create a new arrow from “a person” to “a year” which assigns to each person his or her birth year.
I just wanted to introduce categories and Ologs for later articles.
Cheers – Hein