Christopher Olah wrote an incredibly insightful post on Deep Neural Nets (DNNs) titled “Deep Learning, NLP, and Representations“. In his post, Chris looks at Deep Learning from a Natural Language Processing (NLP) point of view. He discusses how many different deep neural nets designed for different NLP tasks learn the same things. According to Chris and the many papers he cites, these DNNs will automatically learn to intelligently embed words into a vector space. Words with related meanings will often be clustered together. More surprisingly, analogies such as “France is to Paris as Italy is to Rome” or “Einstein is to scientist as Picasso is to Painter” are also learned by many DNNs when applied to NLP tasks. Chris reproduced the chart of analogies below from “Efficient Estimation of Word Representations in Vector Space” by Mikolov, Chen, Corrado, and Dean (2013).
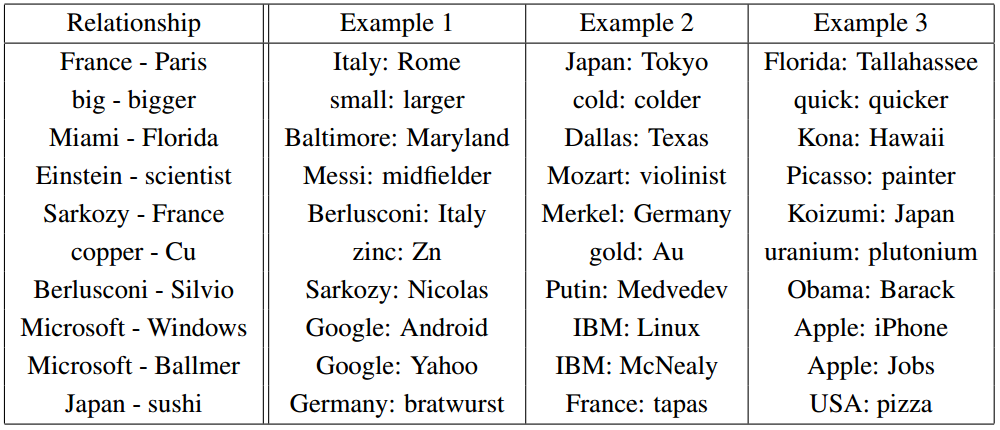
Relationship pairs in a word embedding. From Mikolov et al. (2013).
Additionally, the post details the implementation of recurrent deep neural nets for NLP. Numerous papers are cited, but the writing is non-technical enough that anyone can gain insights into how DNNs work by reading Chris’s post.
So why don’t you just read it like NOW — CLICK HERE. ![]()