http://venturebeat.com/2016/04/05/nvidia-creates-a-15b-transistor-chip-for-deep-learning/
(See also: Half-precision floating-point format )
We're blogging machines!
You are currently browsing the archive for the Technology category.
In case you had not gotten the news yet, the Go playing program AlphaGo (developed by the Deep Mind division of Google) has beaten Lee Se-dol who is among the top two or three Go players in the world. Follow the link below for an informative informal video describing AlphaGo and the victory.
http://www.theverge.com/2016/3/9/11184362/google-alphago-go-deepmind-result
Science magazine has a nice pregame report.
One of my friends showed me his new gaming computer and said that the GPU could do 1.3 teraflops (1.3 trillion floating point operations per second) which is about 500 times faster than my home computer, so I thought, “Imagine how quickly we could search a game tree.” So I started looking around the internet for a super-great GPU chess engine and found basically nothing!! Turns out that the amount of memory per thread is too low, the size of the L1 cache is too small, and the alpha-beta pruning algorithm is not quite parallel enough for GPUs to play chess well. Here is a nice graphic of the L1 access time for a few CPUs and GPUs.
In the paper “Parallel Game Tree Search Using GPU” (2011), L’ubomír Lackovic improved the tree search speed by a factor of two to three by using a GPU instead of the more traditional CPU based tree search for Czech draughts (similar to American Checkers). His tests were based on the ATI Radeon 4890 GPU, the Nvidia GTX460 GPU, and the quad-core processor Intel i5 750 CPU. I had hoped for more speed.
In “Large-Scale Parallel State Space Search Utilizing Graphics Processing Units and Solid State Disks” (2011), von Damian Sulewski invented and test several algorithms for search, reviewed game theory algorithms, and applied GPU processing to several games including “Nine Men’s Morris“. Sulewski used an Intel Core i7 CPU 920 with an NVIDIA GeForce 285 GTX GPU to run his tests. He reported that the GPU was faster by a factor of three to twelve as long as sufficient RAM was available. If the computer ran out of RAM and had to use disk storage, then the GPU performance degraded significantly. He states,
“The observed speed-ups of over one order of magnitude have been obtained (plotted in bold font), exceeding the number of cores on most current PCs. Note that this assertion is true for the dual 6-core CPUs available from Intel, but not on a dual Xeon machine with two quad-core CPUs creating 16 logical cores due to multi-threading. Nonetheless, better speed-ups are possible since NVIDIA GPUs can be used in parallel and the Fermi architecture (e.g. located on the GeForce GTX 480 graphics card) is coming out which will go far beyond the 240 GPU cores we had access to.
For larger levels, however, we observe that the GPU performance degrades. When profiling the code, we identified I/O access as one limiting factor. For example, reading S8,8 from one HDD required 100 seconds, while the expansion of 8 million states, including ranking and unranking required only about 1 second on the GPU.”
So GPU’s are not the silver bullet for games yet.
Robin Hanson gave a very interesting TED talk about a possible technological singularity based on AI and robotics. I outline his talk below and add a few ideas from Hanson’s 1998 article “Long-Term Growth As A Sequence of Exponential Modes“, Ray Kurzweil’s essay (2001) and book (2005), and Bill Joy’s Wired article (2000).
Notes
Hanson’s “Great Eras” graph illustrates major economic revolutions and their effect on growth rates on a log-log scale. Humans doubled their population about every 200,000 years until the agricultural age started 10,000 years ago.1 In the agricultural age, human population and production doubled every 1000 years. Then the industrial revolution occurred and our world economy started doubling every 15 years. Both revolutions increased the growth rate by a factor of 50 to 200. (Kurzweil extends this pattern of revolutions into both the past and the future.)
What if a third major economic revolution occurred? How could it occur?
Robots.
For the past 10,000 years, human economic growth has been based on land, capital, and labor. For the past 200 years we have increased world productivity by population growth, education, and by creating bigger/better tools. Intelligent robots could reproduce more quickly than us, transfer knowledge faster, and they would be their own tools. Robots or artificial intelligences would be so extremely productive that we could experience an economy where our production doubled every month. The amount of stories, art, television, games, science, philosophy, and legal opinions produced would be phenomenal.
Hansen suggest a path to a humanistic robotic world created by this third economic revolution. Artificial intelligence might first be created by mapping the human brain and up-loading human brains into computer hardware. The most productive human individual minds uploaded into computers would proliferate the fastest and thus would dominate. They would be immortal and they would be able to travel across the world quickly and cheaply. Humans would not be able to compete and perhaps we would all retire. The uploaded human minds would live in a beautiful virtual reality.
Hansen describes a society of virtual minds. The most productive minds would acquire or create the most computer resources. Their software personality emulations would run the fastest relative to real-time. He speculates about the structure of this virtual society which includes a caste system, their working habits, and the virtual worlds that the different castes would inhabit.
1This estimate is from “Long-Term Growth As A Sequence of Exponential Modes” and is based on “Population Bottlenecks and Pleistocene Human Evolution” Hawks et al. (2000) and “On the number of members of the genus Homo who have ever lived, and some evolutionary implications” Weiss (1984).
Here’s a link to the video. The tiny “Alien” skull below is printed in less than three minutes.

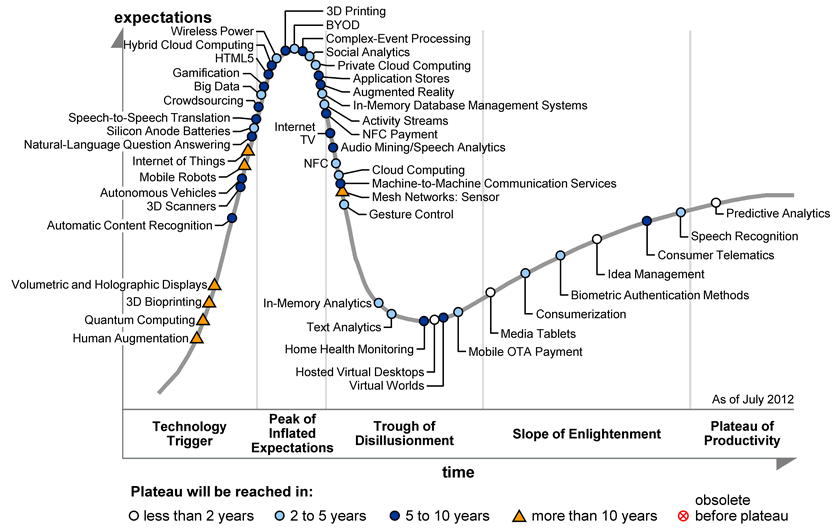
I love this graph. For the complete article, click here.