Artificial Intelligence Blog

“Semantic Hashing”

December 12, 2012 in Deep Belief Networks, Graphical Models, Languages by hundalhh | Permalink

In “Semantic Hashing“, Salakhutdinov and Hinton (2007) show how to classify documents with binary vectors. They combine deep learning and graphical models to assign each document a binary vector. Similar documents can be found by using the L1 difference between the binary vectors. Here is their abstract.

We show how to learn a deep graphical model of the word-count vectors obtained from a large set of documents. The values of the latent variables in the deepest layer are easy to infer and give a much better representation of each document than Latent Semantic Analysis. When the deepest layer is forced to use a small number of binary variables (e.g. 32), the graphical model performs “semantic hashing”: Documents are mapped to memory addresses in such away that semantically similar documents are located at nearby addresses. Documents similar to a query document can then be found by simply accessing all the addresses that differ by only a few bits from the address of the query document. This way of extending the efficiency of hash-coding to approximate matching is much faster than locality sensitive hashing, which is the fastest current method. By using semantic hashing to ﬁlter the documents given to TF-IDF, we achieve higher accuracy than applying TF-IDF to the entire document set.

Cool 3D Printer

December 10, 2012 in Robots, Technology by hundalhh | Permalink

Here’s a link to the video. The tiny “Alien” skull below is printed in less than three minutes.

Technological progress & 3D Printing Hype

December 8, 2012 in Robots, Technology by hundalhh | Permalink

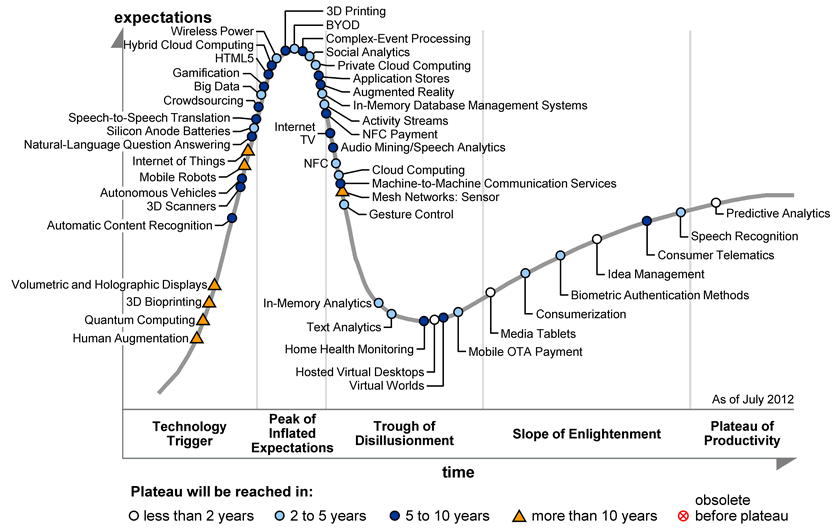
I love this graph. For the complete article, click here.

Product of Experts

December 6, 2012 in Ensemble Learning, Multi-Armed Bandit Problem by hundalhh | Permalink

“A Product of Experts model (PoE) (Hinton 2002) combines a number of individual component models (the experts) by taking their product and normalizing the result.” Here’s the Scholarpedia page.

“Rotation Forest: A New Classifier Ensemble Method”

December 4, 2012 in Ensemble Learning by hundalhh | Permalink

In “Rotation Forest: A New Classifier Ensemble Method“, Rodrıguez and Kuncheva (2006) develop a Random Forest method where the decision boundaries are not of the form original data feature value <= fixed number. They do this by creating new features by “rotating” the data in the high dimensional feature space before creating a decision tree. Each decision tree is created with a different rotation of the data, but all of the rotations are generated from Principal Component Analysis. The trees are combined to generate the final classifier. Here is their abstract

We propose a method for generating classifier ensembles based on feature extraction. To create the training data for a base classifier, the feature set is randomly split into K subsets (K is a parameter of the algorithm) and Principal Component Analysis (PCA) is applied to each subset. All principal components are retained in order to preserve the variability information in the data. Thus, K axis rotations take place to form the new features for a base classifier. The idea of the rotation approach is to encourage simultaneously individual accuracy and diversity within the ensemble. Diversity is promoted through the feature extraction for each base classifier. Decision trees were chosen here because they are sensitive to rotation of the feature axes, hence the name “forest.” Accuracy is sought by keeping all principal components and also using the whole data set to train each base classifier. Using WEKA, we examined the Rotation Forest ensemble on a random selection of 33 benchmark data sets from the UCI repository and compared it with Bagging, AdaBoost, and Random Forest. The results were favorable to Rotation Forest and prompted an investigation into diversity-accuracy landscape of the ensemble models. Diversity-error diagrams revealed that Rotation Forest ensembles construct individual classifiers which are more accurate than these in AdaBoost and Random Forest, and more diverse than these in Bagging, sometimes more accurate as well.

Stochastic Optimization Talk at NIPS

December 4, 2012 in Optimization by hundalhh | Permalink

At NIPS yesterday, James Spall gave a nice overview of stochastic optimization. Stochastic optimization is the process of finding the minimum of a function $f(x)$ where are measurements or samples of the function are noisy. He stressed that the no free lunch theorems (Wolpert & Macready 1995) limit the efficiency of any global minimization problem if there are no restrictions on $f$. He described in detail the Simultaneous Perturbation Stochastic Approximation (SPSA) method which appears to be a great method for optimizing with noisy measurements. The basic is idea is that you don’t need to approximate the gradient by making $p+1$ measurements in a $p$ dimensional domain. Instead, you sample $f$ at two nearby randomly generated points and make a nearly unbiased estimate of the gradient from those two measurements. There is also way to form estimates of the Hessian with just 4 samples which leads to a stochastic algorithm similar to Newton-Raphson. None of these methods can converge faster than $O(1/\sqrt{n})$ due to the noise, but they may be very useful as robust semi-global optimizers for functions with lots of local minima or high frequencies.

Principles for Applying Machine Learning Techniques

December 2, 2012 in General ML by hundalhh | Permalink

Timothy Chklovski at Factual Blog has this cool list of 5 principles for Applying Machine Learning Techniques. His datacentric techniques are:

Don’t Ignore the Corners – The “Corners” are unusual cases in the Data
Be Attentive to the Boundaries – If you use a linear discriminant or decision tree, pay special attention to boundary cases.
Spend Time on Special Cases – i.e. special cases in the data.
Listen to the Data
Love Your Data

Jack Coughlin also at Factual Blog adds this list:

Ask for help first.
The documentation is your best friend.
Know the ecosystem. (Python, Java/Hadoop/Weka, R, Malab, …)
Machine Learning applications are mostly the boring stuff. “The majority of the effort is in pre-processing”
Save the ML for the problems you can’t think to solve in any other way.
Coding in R makes you feel like a ninja. “The R core library is full of awesome one-liners ….”

“Brains, Sex, and Machine Learning”

November 30, 2012 in Deep Belief Networks, Neural Nets by hundalhh | Permalink

Hinton has a new Google tech talk “Brains, Sex, and Machine Learning“. I think that if you are into neural nets, you’ve got to watch this video. Here’s the abstract.

Recent advances in machine learning cast new light on two puzzling biological phenomena. Neurons can use the precise time of a spike to communicate a real value very accurately, but it appears that cortical neurons do not do this. Instead they send single, randomly timed spikes. This seems like a clumsy way to perform signal processing, but a recent advance in machine learning shows that sending stochastic spikes actually works better than sending precise real numbers for the kind of signal processing that the brain needs to do. A closely related advance in machine learning provides strong support for a recently proposed theory of the function of sexual reproduction. Sexual reproduction breaks up large sets of co-adapted genes and this seems like a bad way to improve fitness. However, it is a very good way to make organisms robust to changes in their environment because it forces important functions to be achieved redundantly by multiple small sets of genes and some of these sets may still work when the environment changes. For artificial neural networks, complex co-adaptations between learned feature detectors give good performance on training data but not on new test data. Complex co-adaptations can be reduced by randomly omitting each feature detector with a probability of a half for each training case. This random “dropout” makes the network perform worse on the training data but the number of errors on the test data is typically decreased by about 10%. Nitish Srivastava, Alex Krizhevsky, Ilya Sutskever and Ruslan Salakhutdinov have shown that this leads to large improvements in speech recognition and object recognition.

Hinton has a lot of great ideas in this video including this slide on a massively parallel approach to neural nets.

And this one

And, as mentioned in the abstract, the idea of “dropouts” is very important. (Similar to denoising.)

I wonder if the idea of dropouts can be applied to create more robust Bayesian networks / Probabilistic Graphical Models. Maybe the same effect can be achieved by introducing a bias (regularization) against connections between edges (similar to the idea of sparsity).

Matroids

November 28, 2012 in Math by hundalhh | 2 comments

Matroids are an abstraction of Vector Spaces. Vectors spaces have addition and scalar multiplication and the axioms of vectors spaces lead to the concepts of subspaces, rank, and independent sets. All Vector Spaces are Matroids, but Matroids only retain the properties of independence, rank, and subspaces. The idea of the Matroid closure of a set is the same as the span of the set in the Vector Space.

100 Most useful Theorems and Ideas in Mathematics

November 27, 2012 in Math by hundalhh | 6 comments

So I have been thinking about which ideas in mathematics I use most often and I have listed them below. Please feel free to comment because I would like to use this list as a starting point for a future list of “The most useful ideas in Mathematics for Scientists and Engineers”.

$\ $

I showed this list to Carl and he said his list would be completely different. (He choked a bit when he saw primes at #71.) Hopefully we can post his list as well as others.