A guy named Phil asked me to post my code, so here it is.  It’s in Mathematica, so I imagine that most people will have trouble reading it.  I will probably rewrite the code in a more common, faster language later.

(* Mathematica code for simulating 2048
   - by Hein Hundal (Public Domain)

   Visit  http://gabrielecirulli.github.io/2048/

   for more detials.
*)

(* collapse[v] takes a list of values and returns a 
   collapsed list of values where two consecutive equal 
   values are summed into one value. *)

collapse[v_List] := PadRight[
   collapseAux[Cases[v, _Integer]]  , 4, "."];

collapseAux[{}] = {};
collapseAux[{x_}] = {x};
collapseAux[v_List] := If[ v[[1]] == v[[2]],
   Prepend[ collapseAux[Drop[v, 2]], v[[1]]*2],
   Prepend[ collapseAux[Drop[v, 1]], v[[1]]]];

vGlobalMoves = Characters["lrud"];
mGlobalEmptyBoard = Table[".", {4}, {4}];

move[mBoard_, sMove_String] := Switch[sMove,
   "l", collapse /@ mBoard,
   "r", Reverse /@ collapse /@ Reverse /@ mBoard,
   "u", Transpose[ collapse /@ Transpose[ mBoard ]],
   "d", Reverse[ Transpose[ 
        collapse /@ Transpose[ Reverse[ mBoard]]]],
   _, Throw[{"move::illeagal move", sMove}]];

(* game1Turn[ mStart_List, randFunc_, moveStrat_]
      Performs one turn of the game.
      - mStart is a 4 x4 game matrix where every elemet 
        is either a number 2, 4, 8, ... or the string ".".
      - randFunc is any function that take a positive 
        integer n as input and outputs a positive integer 
        between 1 and n.
      - moveStrat is any function that takes a game board as 
        an input and gives as an output one of the four 
        characters u, d, l, r.
      - The output of game1Turn is a new board state.  *)

game1Turn[ mStart_List, randFunc_, moveStrat_] :=
  Module[{sMove, mBoard, mEmpty, iSpot, iVal},
   sMove = moveStrat[mStart];
   mBoard = move[mStart, sMove];

   (* only add a new piece if the board changed *)
   If[ mBoard =!= mStart,
      mEmpty = Position[mBoard, "."];
      iSpot = randFunc[Length[mEmpty]];

      (* the new board tile will either be a 4 or a 2 *)
      iVal = If[ randFunc[10] == 1, 4, 2];
      mBoard = ReplacePart[mBoard, mEmpty[[iSpot]] -> iVal]
    ];
   mBoard];

(*  gameManyTurns  - executes iDo turns of the game  *)
gameManyTurns[mStart_List, randFunc_, moveStrat_, iDo_Integer] := 
   NestList[game1Turn[#, randFunc, moveStrat] &, mStart, iDo];

(******************* Display Results of Multiple Runs **********)

periodTo0[m_List]  :=  m /. "." -> 0;
maxTile[m_List]    := Max[Flatten[periodTo0[m]]]
totalTiles[m_List] := Total[Flatten[periodTo0[ m ]]];

rand1[i_Integer] := 1 + RandomInteger[i - 1];

(* rand2[m]   replaces a random entry on the board m with a 2 *)
rand2[m_List] := ReplacePart[ m, 
   (RandomInteger[3, {2}] + 1) -> 2];

runSeveralGames[ randFunc_, moveStrat_, iDo_Integer]  := 
   Module[{},
   Table[
    (* run a single game for 100 turns *)
    ten1 = gameManyTurns[rand2[mGlobalEmptyBoard], 
               randFunc, moveStrat, 100];

    (* keep going until there is not change for 50 moves *)
    While[ ten1[[-50]] =!= ten1[[-1]]  && Length[ten1] < 10000,
       ten1 =  Join[ten1, gameManyTurns[ten1[[-1]], 
                    randFunc, moveStrat, 100]]
    ];

    ten2 = TakeWhile[ ten1, # =!= ten1[[-1]] &];

    (* output a list {# turns of the game, tile Total,
    maximum tile} for each game *)
    {Length[ten2], totalTiles[Last[ten1]], maxTile[ten1[[-1]]]},
    {iDo}]];

stats[mRes_List] := Module[{mRN = N@mRes},
   {Mean[mRN], StandardDeviation[mRN], Max[mRes[[All, 3]]],
    Tally[mRes[[All, 3]]] // Sort}];

(******** Blind Cyclic Strategy ****************************)

(* createCyclicStrategy - creates a cyclic strategy function 
   from the string s.  If s = "uddl", then the strategy function 
   will repeat the sequence move up, move down, move down, and 
   move left indefinitely. *)

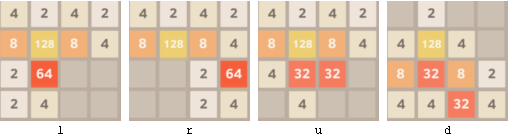
createCyclicStrategy[sMoves_String] := Module[
   {exHeld, iCount = 1},
   exHeld = Hold[
     Function[ m, chars[[ Mod[iCount++, iStringLength] + 1]]]];
   ReleaseHold[
    exHeld /. {chars -> Characters[sMoves] ,
      iStringLength -> StringLength[sMoves]}]];

testOneStrategy[] := Module[{},
   stratDRDL = createCyclicStrategy["drdl"];
   mRes = runSeveralGames[rand1, stratDRDL, 100];
   stats[mRes]];

In my last post, I described how to play 2048 and reported the results of some simple simulations.  Namely, I reported the results of two very simple strategies:

• Random play will achieve an average ending tile total (AETT) of 252 and usually the highest tile will be a 64 tile or a 128 tile (about an 85% chance of ending with one of those).
• A pure greedy strategy where the player just tries to make the largest new tile possible results in an average ending tile total (AETT) of 399 and usually the highest tile will be a 128 tile or a 256 tile (about an 87% chance of ending with one of those).

Blind Strategies

Perhaps surprisingly, there are “blind” strategies that will do even better than the pure greedy strategy.  Blind strategies are strategies that ignore the current state of the board.  I tried two types of simple blind strategies “biased random” and “repeating sequences”.  I will summaries the results of the biased random trials in my next post.

The simplest repeating strategy would be just hitting the same key every time—down, down, down, ….   Of course that does not do well.  Nor would down, up, down, up, ….  So the simplest repeating strategy worth trying would be down, right, down, right or some other combination of horizontal and vertical moves.  I ran 100 games for every possible repeated sequence of two to four moves and found that the best of these sequences was down, right, down, left  or a version of that sequence in disguise.  The results are captured in the table below.

Notice that restricting your moves to only two out of the four possibilities does poorly.  The Down, Left, Down, Left… strategy had an average tile total of only 44.38 at the end of the game and that strategy never created a tile above 64.

The best strategies were down-right-down-left or that same strategy in disguise (dlul, dldr, and drur are really the same strategy).  Notice that this strategy does better than pure greedy which had an AETT of 399.

What would you do with 2880 cores?

Vasik Rajlich, author of the legendary chess program Rybka,  used them to show that chess champion Bobby Fisher was right about the chess opening King’s Gambit (see “A bust for King’s Gambit“) .

King’s Gambit

Vasik proved that King’s Gambit is a loss for white unless white plays 3. Be2 after black takes the pawn.  (In that case, it’s a draw.)  For the details, click on the link below.

http://en.chessbase.com/post/rajlich-busting-the-king-s-gambit-this-time-for-sure