In the game Master of Orion and some related games, it is possible to purchase technologies that increase the rate of growth of your empire. I wanted to simplify this idea enough to get clean mathematical solutions. I call the resulting three simplified games the first, second, and third banker’s problems.
- In the first banker’s problem, the saver is offered a deal where they can buy an interest rate upgrade for a fixed amount of money paid from the account balance at any time specified by the saver.
- The second banker’s problem is the same as the first, except that the payment for the interest upgrade comes solely from account interest.
- For the third banker’s problem the saver can, at any time, upgrade from interest rate $r_1$ to interest rate $r_2$ for $c_1$ dollars and upgrade from $r_2$ to $r_3$ for $c_2$ dollars, or upgrade directly from interest rate $r_1$ to interest rate $r_3$ for $c_2$ dollars where $r_1<r_2<r_3$ and $c_1<c_2$.
This post will state the formula for computing the optimal time to buy the interest rate upgrade for the first banker’s problem, compute the optimal time to buy for one example, and show the results of buying at non-optimal times.
All of the formulas and theorems about the first banker’s problem as well as Python simulation code for the first banker’s problem and proofs can be found in this PDF.
the first banker’s problem
Consider the following game. You have a bank account that is compounded continuously with an interest rate of $r_1$. Your banker offers you the following deal. At any time in the future, if your account balance is greater than $c$ dollars, you can pay $c$ dollars from the account to increase your interest rate to $r_2$. You can only use the funds in the account to pay for this interest rate increase and you can never add or subtract any money until retirement which is very far in the future. When should you accept the banker’s offer? (We assume that $c, r_1,$ and $r_2$ are positive real numbers and $1>r_2> r_1>0$.)
At first you might be tempted to say that you should buy the interest rate increase as early as possible, but it turns out that that is a bad idea. If you have exactly $c$ dollars in the account and you buy the rate increase, then you will have zero dollars in the account and you are stuck with zero dollars in the account until you retire. Similarly, if you have $c+\$0.01$ in the account and you buy the interest rate increase, then you will only have one cent in the account after the purchase, and it will take a long time to grow that one cent into a large amount of money.
On the other hand, it is probably wrong to wait until the last microsecond before you retire to buy an interest rate increase because the increased amount of interest that you receive is unlikely to be larger than the cost $c$.
The answer to the first banker’s problem is that you should take the deal at time
\begin{equation}
t_{\mathrm{buy}}=\frac{1}{r_1}\ln\left(\frac{c \; r_2 }{B_0(r_2-r_1)}\right)
\end{equation}
where $B_0$ is the amount of money in the account at time zero, and $\ln(x)$ is the natural log. $$\ln(x) = \frac{\log_{10}(x)}{\log_{10}(e)}.$$
At that time the balance before the purchase will be
\begin{equation}
\mathrm{balanceBefore} =\frac{c \; r_2 }{r_2-r_1},
\end{equation}
and the balance immediately after purchasing the interest upgrade will be
\begin{equation}
\mathrm{balanceAfter} =\frac{c \; r_1 }{r_2-r_1}.
\end{equation}
Example
For example, if
- you initially have \$1000 in the account,
- the cost of increasing the interest rate is \$1,100,
- $r_1=0.05=5\%$, and
- $r_2=0.08=8\%$,
then the the correct time to buy the interest rate increase is
$$
\begin{aligned}
t_{\mathrm{buy}}&=\frac{1}{r_1}\ln\left(\frac{c \; r_2 }{B_0(r_2-r_1)}\right)\\
&=\frac{1}{0.05}\ln\left(\frac{1100\cdot 0.08 }{1000(0.08-0.05)}\right)\\
&=\frac{1}{0.05}\ln\left(\frac{88 }{1000(0.03)}\right)\\
&=20\ln\left(\frac{88 }{30}\right)\\
&\approx21.5228\ \mathrm{years}
\end{aligned}
$$and the account balance before making the payment at the optimal time would be
$$\begin{aligned}\mathrm{balanceBefore} &=\frac{c \; r_2 }{r_2-r_1}\\&=\frac{1100 \cdot 0.08 }{0.08-0.05}\\&=\frac{88 }{0.03}\\&\approx \$2933.33.\end{aligned}$$
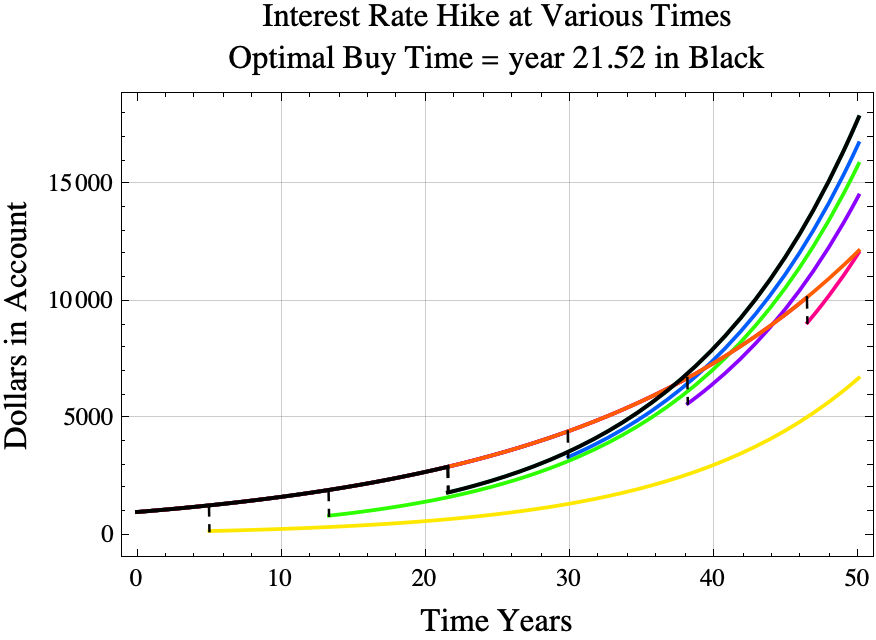
The diagram below shows what happens if you buy the interest upgrade at various times. The purchases are represented as a black vertical dashed lines. The solid black line shows the results of paying \$1,100 at year 21.5228, the optimal time to invest. The red line shows what happens if the player does not invest before year 50. The yellow line shows the result if she or he invests on year 5.