Consider the following game. You have a bank account that is compounded continuously with an interest rate of $r_1$. Your banker offers you the following deal. At any time in the future, you can pay $c$ dollars using only the interest from the account to increase your interest rate to $r_2$. If your balance is $b$ at the time of the upgrade, then your balance will remain at $b$ for $c/(r_1 b)$ years which is the time required to pay $c$ dollars from interest alone. Other than paying for the interest upgrade, you can never add or subtract any money until retirement which is very far in the future. When should you accept the banker’s offer? Let’s call this game “the second banker’s problem”. (We assume that $c, r_1,$ and $r_2$ are positive real numbers and $1>r_2> r_1>0$.)
(This game is similar to purchasing a growth technology in the game Master of Orion (Original 1993 version). For example, if you buy the “Improved Industrial Tech 9″ technology early in the game, the cost of factories is reduced for the remainder of the game. Reducing the cost of factories increases your economy’s growth rate.)
(All proofs for the second banker’s problem can be found in this PDF.)
For the first banker’s problem, the balance in the account is immediately reduced by $c$ dollars and the interest rate is immediately increased to $r_2$. See this blog post or this PDF for an analysis of the first banker’s problem. The third banker’s problem allows the saver to buy two separate interest rate increases.
For the second banker’s problem, you might be tempted to say that you should buy the interest rate increase as early as possible, but that might be bad if $c/(r_1 b)$ is a large number of years. On the other hand, there is no reason to buy the interest rate upgrade if the time to retirement is less than $c/(r_1 b)$ years.
Optimal Purchase Time
Perhaps surprisingly, the optimal time to purchase the interest rate hike is the same for the first and the second banker’s problems. For either problem, you should take the deal at time
$$t_{\mathrm{buy}}=\frac{1}{r_1}\ln\left(\frac{c \; r_2 }{B_0(r_2-r_1)}\right)$$
where $B_0$ is the amount of money in the account at time zero, and $\ln(x)$ is the natural log. $$\ln(x) = \frac{\log_{10}(x)}{\log_{10}(e)}.$$ I was a bit surprised to find that the optimal purchase time $t_{\mathrm{buy}}$ for the second banker’s problem is the same as the optimal purchase time for the first banker’s problem.
The amount of money in the account at the optimal purchase time is $$b_{\mathrm{opt}} = \frac{c \; r_2 }{r_2-r_1}.$$
Example
For example, if
- you initially have \$1000 in the account,
- the cost of increasing the interest rate is \$1,100,
- $r_1=0.05=5\%$, and
- $r_2=0.08=8\%$,
then the the correct time to buy the interest rate increase is
$$
\begin{aligned}
t_{\mathrm{buy}}&=\frac{1}{r_1}\ln\left(\frac{c \; r_2 }{B_0(r_2-r_1)}\right)\\
&=\frac{1}{0.05}\ln\left(\frac{1100\cdot 0.08 }{1000(0.08-0.05)}\right)\\
&=\frac{1}{0.05}\ln\left(\frac{88 }{1000(0.03)}\right)\\
&=20\ln\left(\frac{88 }{30}\right)\\
&\approx21.5228\ \mathrm{years.}
\end{aligned}
$$
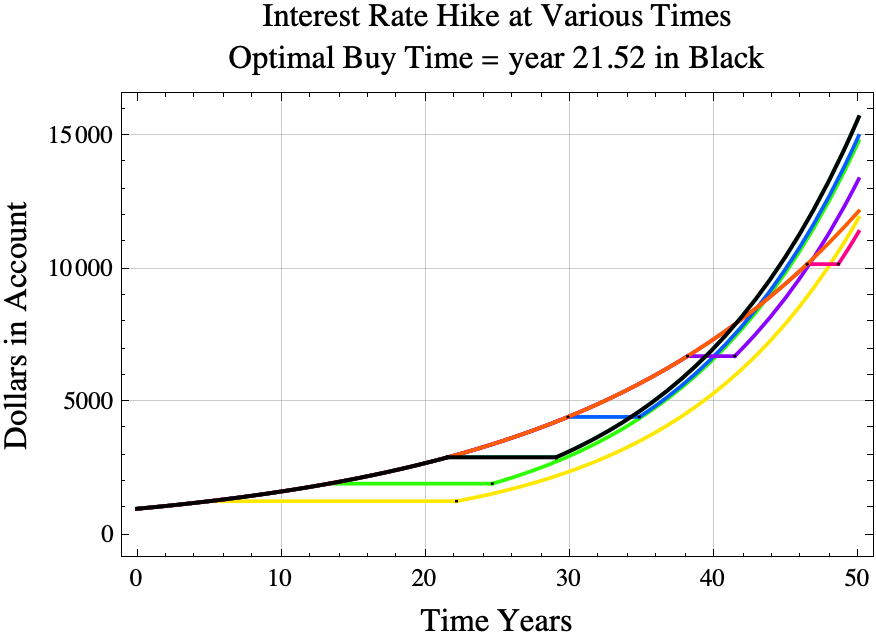
In the diagram above, the black line shows the results of paying \$1,100 from interest starting at year 21.5228, the optimal time to start paying for the interest rate upgrade. The orange line shows what happens if the player does not invest before year 50. The yellow line shows the result if she or he starts paying for the investment on year 5.