In part 1, we described the “first banker’s problem” where you can pay a banker to increase your interest rate from $r_1$ to $r_2$ by removing $c$ dollars from your account. The optimal time to purchase the rate increase is when you have
\begin{equation}
\mathrm{balanceBefore} =\frac{c \; r_2 }{r_2-r_1}
\end{equation}
dollars in your account. (All of the formulas and theorems about the first banker’s problem as well as Python simulation code for the first banker’s problem and proofs can be found in this PDF.)
Interest Income immediately before the optimal purchase time
When compounding continuously, the amount of interest that you are earning at any time is the balance at that time times $r_1$. The amount of interest income just before the optimal purchase time is
$$\mathrm{interst\ income\ immediately\ before\ purchase} = r_1\cdot \mathrm{balanceBefore} = \;\frac{r_1 r_2 c}{r_2-r_1}.$$
example
If
- you initially have \$1000 in the account,
- the cost of increasing the interest rate is \$1,100,
- $r_1=0.05=5\%$, and
- $r_2=0.08=8\%$,
then
$$
\begin{aligned}
\mathrm{income\ immediately\ before\ purchase} &= \frac{c \;r_1 r_2 }{r_2-r_1}\\
&= \frac{ \$1100\cdot 0.05 \cdot 0.08}{0.08-0.05}\\
&= \frac{ \$55 \cdot 0.08}{0.03} \approx \$146.67\mathrm{\ per\ year.}
\end{aligned}
$$
Recovery Time
If you do purchase the interest rate hike at the optimal time, how many years will you need to wait until the optimal strategy surpasses the never buy strategy? The answer is you will have to wait approximately $1/m$ years after the purchase where $m$ is the average of $r_1$ and $r_2$. The exact time when the optimal strategy surpasses the never buy strategy is
$$
t_{\mathrm{surpass}} = t_{buy} + \frac{ \ln(r_2) – \ln(r_1)}{r_2-r_1}.
$$where $$t_{\mathrm{buy}}=\frac{1}{r_1}\ln\left(\frac{c \; r_2 }{B_0(r_2-r_1)}\right)$$
and $B_0$ is the amount in the account at time 0. (Bounds for the expression $(\ln(r_2) – \ln(r_1) )/ (r_2 – r_1)$ can be found here.)
For the previous example,
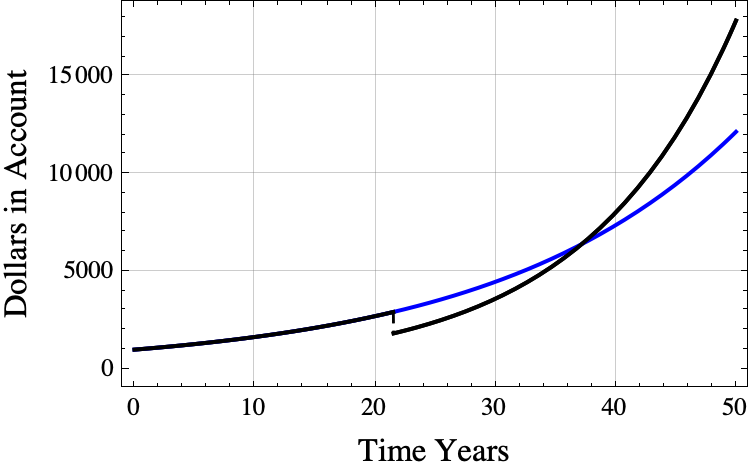
$$t_{\mathrm{surpass}} \approx 21.5228+ \frac{ \ln(0.08) – \ln(0.05)}{0.08-0.05} \approx 37.1868.$$
The black line shows the results of buying the interest rate at the optimal time. The blue line shows what happens if you never buy the interest rate hike and just continue to get 5% interest.
The number of years needed to catch up is between $1/r_2$ years and $1/r_1$ years. GPT wrote a nice proof of this fact.
If you buy the interest rate hike at the optimal time, then you will maximize the account balance at all times $t>1/r_1$ years later. (Mathematically, for every $t> t_{\mathrm{buy}} + 1/r_1$, the strategy of purchasing the interest rate upgrade at time $t_{\mathrm{buy}}$ results in an account balance at time $t$ that exceeds the account balance at time $t$ using any other strategy.