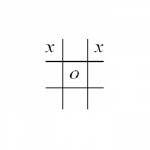So far we have only considered blind strategies and a simple greedy strategy based on maximizing our score on every move. The results were interesting because the blind cyclic strategy left-down-right-down did surprisingly well and we saw that a biased random strategy which strongly favored two orthogonal moves like left and down with a small amount of one other move like right outperformed all of the other biased random strategies.
If we want to do better, we need something more sophisticated than a blind strategy or pure, short-term, score greed.
The first approach used by game AI programmers in the olden days was to simply program in the ideas that the programmer had about the game into the game AI. If the programmer liked to put an X in the middle of a tic-tac-toe board, then he hard-wired that rule into the computer code. That rule alone would not be enough to play tic-tac-toe, so the programmer would then just add more and more decision rules based on his own intuition until there were enough rules to make a decision in every game situation. For tic-tac-toe, the rules might have been
- If you can win on your next move, then do it.
- If your opponent has two in a row, then block his win.
- Take the center square if you can.
- Take a corner square if it is available.
- Try to get two squares in a single row or column which is free of your opponent’s marks.
- Move randomly if no other rule applies.
Though this approach can be rather successful, it tends to be hard to modify because it is brittle. It is brittle in two ways: a new rule can totally change the behavior of the entire system, and it is very hard to make a tiny change in the rules. These kind of rule based systems matured and incorporated reasoning in the nineties with the advent of “Expert Systems“.
Long before the nineties, the first game AI programmers came up with another idea that was much less brittle. If we could just give every position a numerical rating, preferably a real number rather than an integer, then we can make small changes by adding small numbers to the rating for any new minor feature that we identify.
In tic-tac-toe, our numerical rating system might be as simple as:
- Start with a rating of zero
- Add 100 to the rating if I have won,
- Subtract 100 if my opponent has won or will win on his next move,
- Add 5 if I own the central square,
- Add 2 points for each corner square that I own,
- Add 1 point for every row, column, or diagonal in which I have two squares and my opponent has no squares.
So, for example, the position below would be scored as
2 (for the upper left corner x) + 2 (for the other corner) + 1 (for the top row) = 5.
Now, in order to decide on a move, we could just look at every possible move, rate each of the resulting boards, and choose the board with the highest rating. If our tic-tac-toe position was the one below and we were the x player,
then we would have six possible moves. Each move could be rated using our board rating system, and the highest rated board with x in the center and a rating of 8 would be chosen.
This approach was first applied to computer game AI by the famous theoretician Claude Shannon in the paper “Programming a Computer for Playing Chess” (1949), but the idea without the computers actually predates Shannon by hundreds of years. For instance, the chess theoretician Giambatista Lolli published “Osservazioni teorico-pratiche sopra il giuoco degli scacchi ossia il Giuoco degli Scacchi” in 1763. He was the first to publish the idea of counting pawns as 1, bishops as 3, knights as 3, rooks as 5, and queens as 9 thereby giving a rating to every board position in chess (well, at least a rating for the pieces). Shannon modified this rating by subtracting 0.5 for each “doubled” pawn, 0.5 for each “isolated” pawn, 0.5 for each “backward” pawn, and adding 0.1 for each possible move. Thus, if the pieces were the same for both players, no captures were possible, and if the pawns were distributed over the board in a normal fashion, Shannon’s chess AI would choose the move which created the most new moves for itself and removed the most moves from his opponent.
Shannon significantly improved on the idea of an evaluation function by looking more than one move ahead. In two players games, the main algorithm for looking a few moves ahead before applying the evaluation function is the alpha-beta search method which will be tested in a later post.
Let’s try to find and test a few evaluation functions for 2048.
Perhaps the simplest idea for evaluating a position is related to flying. According the great philosopher Douglas Adams,
“There is an art to flying, or rather a knack. Its knack lies in learning to throw yourself at the ground and miss. … Clearly, it is this second part, the missing, that presents the difficulties.” (HG2G).
Suffice it to say that in 2048, the longer you delay the end of the game (hitting the ground), the higher your score (the longer your flight). The game ends when all of the squares are filled with numbers, so if we just count every empty square as +1, then the board rating must be zero at the end of the game.
I ran 1000 simulated games with the Empty Tile evaluation function and got an average ending tile total of 390. The strategy ended the games with a maximum tile of 512 tile 25 times, a 256 tile 388 times, 128 491 times, 64 92 times, and 32 4 times.
Well, that didn’t seem like anything spectacular. Let’s try to group like tiles—if there are two 128 tiles, let’s try to put them side-by-side. Of course, the idea of putting like tiles together is obvious. Slightly less obvious is the idea of trying to put nearly equal tiles together. Over at stackoverflow.com, the user ovolve, the author of the first 2048 AI, suggested the criteria of “smoothness” in his great post about how his AI worked. There are some interesting ways to measure smoothness with Fourier transforms, but just to keep things simple, let’s measure smoothness by totaling the differences between side-by-side tiles. For example, the smoothness of the board below would be
2+2+4 (first row) + 30+32 (second row) + 14+ 48 + 64 (third row) + 12 + 16 (fourth) + 2+0+2 (first col) + 30+16 + 0 (second) + 4 + 64 + 64 + 128 + 128
which sums to 662.
Once again I ran a 1000 games using smoothness as an evaluation function. The average ending tile total was 720, a new high. The strategy had a maximum ending tile total of 1024 3 times, 512 263 times, 256 642 times, 128 87 times, and 64 5 times. This looks very promising.
Let’s try ovolve’s last criteria — monotonicity. The idea of monotonicity is that we prefer that each row or column is sorted. On the board above, the top row
4 > 2 < 4 > 0 is not sorted. The second 2 < 32 > 0 = 0 and forth 4 < 16 > 0 = 0 rows are sorted only if the spaces are ignored. The third row 2 < 16 < 64 < 128 is fully sorted. Let’s measure the degree of monotonicity by counting how many times we switch from a less than sign to a greater than sign or vice-versa. For the first row we get 2 changes because the greater than sign 4 > 2 changed to a less than sign 2 < 4 and then changed again in 4 > 0. We also get two changes for 2 < 32 > 0, no sign changes in the third row (perfectly monotonic), and two changes in the last row.
I ran 100 games using the monotonicity evaluation function. The average ending tile total was 423. The maximum tile was 512 16 times, 256 325 times, 128 505 times, 64 143 times, and 32 11 times.
I have summarized the results of these three simple evaluation functions in the table below.
| Evaluation Func | AETT | Max Tile |
|---|---|---|
| Empty | 390 | 512 |
| Smoothness | 720 | 1024 |
| Monotonicity | 420 | 512 |
| Cyclic LDRD | 680 | 512 |
| Pure Random | 250 | 256 |
Well, clearly Smoothness was the best.
There are three great advantages to numerical evaluation functions over if-then based rules. One, you can easily combine completely different evaluation functions together using things like weighted averages. Two, you can plot the values of evaluation functions as the game proceeds, or even plot the probability of winning against one or two evaluation functions. Three, in 2048, there is the uncertainty where the next random tile will fall. With numerical evaluation functions, we can average together the values of all the possible boards resulting from the random tile to get the “expected value” (or average value) of the evaluation function after the random tile drop.
Well, that’s it for my introduction to evaluation functions. Next time we will focus on more sophisticated evaluation functions and the powerful tree search algorithms that look more than one move ahead.
Have a great day. – Hein